FIR-Filter¶
An FIR filter is a nonrecursive filter having an impulse response that lasts for a limited duration, meaning it reaches zero after a finite amount of time. All feedforward digital filters are FIR filters. The impulse response of an Nth order/tap FIR filter takes precisely N+1 samples to settle to zero. There is no analog counter-part for FIR filter. FIR filters are easy to implement in software. FIR filters are non-recursive in nature.

Fig 1: Logical structure of FIR filter. Block z-1 represent delay using z-transforms.
The filter shown above can be mathematically represented as follows :
$$H(z)=\sum_{n=0}^{N-1}h(n)z^{-n}$$
An FIR filter (as shown above) has only forward path. There is no feedback path, so an FIR filter is always stable. It can be observed that FIR filters have only zeros and no poles. It can achieve linear phase response preventing signal distortion which cannot be achieved in feedback filters (IIR filter) or analog filters.
The non-zero values of the impulse response takes the values of the coefficients.
Moving average filter¶
The simplest form of digital filters is finite impulse response filter. Most elementry form of FIR filter is a moving average filter. A moving average filter has equal weights.
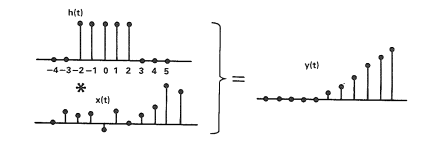
Fig 2: Convolution of moving average filter with a signal. (Source : Analog Devices)
Number of Taps¶
The number of taps represents the number of samples or the number of stages. Increasing the number of taps sharpens the rolloff characteristics of the filter.
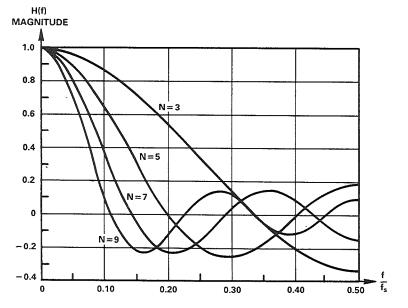
To increase the sharpness further, individual weights can be assigned instead of assigning constant values to each of them.
z-transform of an FIR filter¶
For a N-tap FIR filter with h(k) coefficient, then the output is defined as
$$y(n)=h(0)x(n)+h(1)x(n-2)+\dots{}+h(n-1)x(n-N-1)$$
The z-transform of the filter is
$$H(z)=h(0)z^{-1}+h(1)z^{-1}+h(2)z^{-2}+\dots{}+h(N-1)z^{-(N-1)}$$
or,
$$H(z)=\sum_{n=0}^{N-1}h(n)z^{-n}$$
Types of FIR filter¶
On the basis of filtering characteristics¶
On the basis of coefficients¶
- Boxcar
- Hilbert transformer
- Lth Band
- Raised cosine